[강화학습] Model Free Prediction: Monte-Carlo, Temporal Difference, SARSA

 

 이전에 배웠던 MDP는 보상과 상태 변환 확률 등 환경의 정보를 안다는 가정하에만 진행할 수 있다는 한계가 존재한다. Model-Free Reinforcement Learning이란 환경 정보가 알려진 MDP와 달리, 직접 환경과 상호작용하며 value를 예측하고 최적화하는 학습 방법이다. 이 과정에서 value를 예측하고 평가하는 것을 'Model-Free Prediction'이라고 하며, 예측에는 크게 '몬테카를로 예측'과 '시간차 예측'이 있다. value를 최적화하는 것은 'Model-Free Control'이라고 하며, 시간차 제어의 일종인 'SARSA'가 있다. 

 

---

1. Monte-Carlo Methods

 

주요 특징

• MDP transitions나 rewards에 대한 정보는 모르는 상태(model-free)
• 경험에 의해서 직접적으로 학습함
• 완전한 에피소드(starting state~termination state)를 학습함으로써 얻어지는 평균적인 return을 value값으로 사용
• No Bootstraping(이전에 구했던 값에 의존하지 않는 성질)

 

Monte-Carlo Policy Evaluation

기존에 Dynamic Programming 방식에서 value function을 추정할 때, 미래 보상에 대한 누적 기댓값을 사용했다. 그러나 Model-Free한 환경에서는 state probability나 reward 등의 정보가 주어져있지 않기 때문에, 미래에 받을 것으로 기대되는 값을 예측(계산)하기 어렵다. 아래와 같이 특정 상태에서의 가치함수를 계산하기 위해서 변형된 벨만 기대 방정식을 살펴본다면, 결국 환경의 모델인 '상태 변환 확률(P)'과 '보상값(Rt+1)'을 알아야만 가치함수를 알아낼 수 있다는 점을 확인할 수 있다.

 

 

 

이러한 한계를 해결하기 위해 "근사"라는 방식을 활용해 가치함수를 추정해보고자 하고자한다. 즉 Monte-Carlo의 기본적인 개념은 episode를 끝까지 가본 다음, 그 과정에서 얻어진 reward들로 각 state의 value function을 거꾸로 계산해보는 것이다. 첫 state에서 마지막 state까지 가는 하나의 episode는 결국 하나의 sample이라고 볼 수 있으며, 여러 번의 샘플링을 통해 얻은 평균으로 가치함수의 값을 추정한다. 

 

또한 Dynamic Programming 방식과 달리 이전에 얻어진 정보에 의존하여 추정하는 것이 아니므로 Boostraping 방식이 아니라고 한다. 

 

• 목표 : policy π 하에서 경험을 통해 발견한 정보를 통해 Vπ(s) 학습 *Planning : 모든 state, MC = 경험한 state한정 

• 반환값 G : 시작점부터 종점까지 완전한 episode를 통해 학습하므로, total discounted reward

• Monte-Carlo Policy evaluation은 경험으로 얻어진 평균 반환값을 사용

• 하나의 Episode에서 얻은 반환값의 평균값으로 value function을 추정하고, episode를 여러 번 반복한다면 좋은 estimation 결과를 얻을 수 있다는 것이 아이디어이다. 
• 즉 아래의 식은 여러 번의 에피소드에서 S라는 상태를 방문해서 얻은 반환값들의 평균을 통해 가치함수를 추정하는 것이다. 이 때 n은 상태 S를 여러 번의 에피소드 동안 방문한 횟수이다. 

 

 

• 또한 식을 정리했을 때, 어떤 상태의 가치함수는 샘플링을 통해 에이전트가 그 상태를 방문할 때마다 1/n(G(S)-V(S)) 만큼 업데이트 됨을 알 수 있다. 이 때 G(S)-V(S)를 오차라고 하며, 1/n을 step size라고 한다. 이 step size를 일반화하여 α로 표현할 수 있으며, α가 너무 크면 수렴하지 못하고 너무 작으면 수렴속도가 느리게 된다.
• 어떤 상태의 가치함수가 업데이트될 수록 가치함수는 현재 정책에 대한 참 가치함수에 수렴해가며, 몬테카를로 예측에서 최종적인 업데이트 목표는 G(s)로 다가가는 것이다.
• 몬테카를로 예측(Monte-Carlo Prediction) 이후의 강화학습 방법에서 가치함수를 업데이트하는 방식은 해당 수식의 변형이므로, 이를 잘 알아두도록 해야한다.

 

---

 

State를 평가하는 방법에 따라서 아래와 같이 두 가지로 분류할 수 있다.

 

  1) First-Visit Monte-Carlo Policy Evalution

• 에피소드에서 하나의 state를 여러 번 거쳐갈 수 있다. ex. S1(Start)-S2-S1-S4-S5(Terminate)
• 이 때 특정 state에 처음으로 방문했을 때(First time-step t)의 value값만 추정에 사용하는 방식이다.
• Value값인 V(s)는 평균 return 값으로 S(s)/N(s)이다.
• N(S) : total episode동안 state s를 방문한 횟수이다.
• N(S)가 무한대로 간다면, V(s)도 true value function으로 수렴한다. 

 

 

  2) Every-Visit Monte-Carlo Policy Evalution

• 특정 state를 여러번 방문했을 때에도 Increment counter와 return 값에 포함시킨다.
• 방문할 때마다 바뀐 return값이더라도 넣어준다.

  

(예시) Mars Rover
*Policy : 모든 states에서 왼쪽으로 이동
*Reward : -1 every movement, +1 arriving at S1
*Discount factor : 0.5
*환경의 모델을 알지 못한다고 전제

이러한 전체하에 Sample episode는 (S2, S3, S2, S1)와 (S2, S1)으로 2가지가 주어졌다고 하자.

 

1) First-Visit MC

Episode (S2, S3, S2, S1)와 (S2, S1)에서 S2가 총 3번 나왔음에도 불구하고, N(S2) = 3으로 계산하지 않는다. 첫번째 에피소드에서 S2가 2번 등장했음에도 불구하고, 1번만 카운트 한 것이다.

 

	Episode 1에서의 V(S)		Episode 2에서의 V(S)
	S2	S3	S2
N(S)	N(S2) =1	N(S3) = 1	N(S2) = 2
V(S)	V(S2) =  (-1 + 0.5*-1+ 0.5^2*1) / 1 = -1.25	V(S3) = (-1 + 0.5*+1) / 1         = -0.5	V(S2) = (-1.25+1)/2         = -0.125
설명	S2 → S3 reward : -1 S3 → S2 reward : -1 S2 → S1 reward : 1	S3 → S2 reward : -1 S2 → S1 reward : 1	S2 → S1 reward : 1 N(s) ← N(s) + 1  S(s) ← S(s) + Gt

 

 

2) Every-Visit MC

Episode (S2, S3, S2, S1)와 (S2, S1)에서 S2가 총 3번 나왔기 때문에 N(S2) = 3으로 계산하였으며, 첫 S2가 등장했을 때를 기준으로 끝까지 episode를 방문했을 때 얻은 return값 -1.25, 두번째 S2가 등장해 끝까지 갔을 때의 return값 1을 모두 반영해주고 있음을 알 수 있다. 

 

	Episode 2에서의 V(S)
	S2
N(S)	N(S2) = 3
V(S)	V(S2) = (-1.25+1+1)/3 = 0.25

 

---

Incremental Monte-Carlo Update

위에서 언급한 Incremental Mean을 한 번 더 살펴보자. 즉 k번째의 평균값은 k-1번째까지의 평균값을 알고 있을 경우 구할 수 있다는 것이다. 새로운 Xk라는 Sample을 얻었을 때, 그 sample과 이전의 평균값의 차를 통해 계산할 수 있다.

 

하나의 에피소드가 완료되면 Value function을 업데이트 한다. 위에서 표현한 식을 차용한다면, 업데이트 되는 Value function V(St)는 결국 직전까지의 value function과 방금 얻은 새로운 sample을 통해 구할 수 있게 된다. 또한 N(S)가 커짐에 따라, 1/N(S)은 점점 작아지게 되고 Increment한 값은 덜 반영이 되며, 결과적으로 V(s)가 수렴할 수 있게 되는 것이다. 

참고로 환경에 따라서 N(S)값이 급격하게 커져버리면, 1/N(S)값이 급격히 작아져 새로운 Sample값인 G를 반영하지 못하게 되는 상황이 발생할 수 있다. 이처럼 running mean을 일정하게 tracking하여 학습을 하고자 한다면, 특정한 알파값을 설정하여 조절할 수 있다. 

 

---

2. Temporal Difference Learning

 

앞서서 설명한 몬테카를로 예측은 가치함수를 업데이트하기 위해 에피소드가 끝날 때까지 기다려야 하므로, 에피소드의 길이가 매우 길거나 끝나지 않을 경우 상당한 단점으로 작용한다. 따라서 이를 극복하기 위해 매 에피소드마다 업데이트를 하는 것이 아니라, 좀 더 짧은 주기인 타임스텝(time step)마다 가치함수를 업데이트하는 방법이 바로 시간차 예측(Temporal Difference prediction)이다. 

 

시간차예측에서는 에피소드를 다 끝냈을 때야 얻을 수 있었던 Gt 대신, R+γV(St+1)로 나타낸 가치함수의 정의를 활용한다. R+γV(St+1)값을 샘플링하여, 현재의 가치함수를 업데이트하는 것이다. 어떤 상태에서 행동을 하면 보상을 받고, 다음 상태를 알게 되는데 이 때 얻은 보상에 다음 상태의 가치함수를 더한 값을 업데이트의 목표로 삼고 있다. 또한 다른 상태의 가치함수를 통해 현재 상태의 가치함수를 예측하므로, 부트스트랩(bootstrap)방식이라고도 할 수 있다. 

 

또한 시간차예측에서의 가치함수 업데이트는 실시간으로 이루어지므로, 한 번의 하나의 가치함수만 업데이트가 된다. 이 때 R+γV(St+1)을 TD target, R+γV(St+1)-V(S)는 TD error(시간차에러)라고 한다. 

 

---

3. Temporal Difference Control & SARSA

 

시간차예측에서 가치함수를 참가치함수로 다가가도록 업데이트 함으로써 '평가'의 과정을 거쳤다면, 현재의 상태에서 가장 큰 가치를 지니는 행동을 선택함으로써 정책을 '발전'시켜야 할 것이다. 다만, 몬테카를로 예측 뿐만 아니라, 시간차예측에서는 환경의 모델인 상태변환확률(P, state transition probabiliy)를 알 수 없기 때문에 기존의 '가치 이터레이션(value iteration)'에서의 수식을 사용하기 어렵다. 대신 현재 상태의 Q함수를 통해서는 상태변환확률을 모르더라도 판단할 수 있을 것이다. 

 

value iteration에서의 정책발전

 

한편 최대의 Q값을 만드는 행동을 선택하려면, agent는 상태가치함수가 아닌 Q함수의 정보를 알아야 하므로, 시간차 제어에서의 업데이트 대상은 상태가치함수가 아닌 Q함수가 되어야할 것이다. 아래 수식에서 볼 수 있듯이, 시간차제어에서 Q함수를 업데이트하려면 다음 상태 St+1과 그 때의 행동 At+1을 알고 있어야 한다. 즉 Q함수를 업데이트하기 위해서는 [St, At, Rt+1, St+1, At+1]라는 샘플 정보를 가지고 있어야 한다. 이 샘플들의 앞 글자인 S,A,R,S,A를 따와서 시간차제어를 살사(SARSA)라고도 한다. 이러한 샘플을 탐욕 정책을 기반으로 모으고, 샘플로 큐함수를 업데이트하는 과정을 반복하는 것이다. 

 

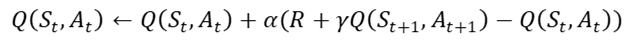
다만, agent가 많은 경험을 하기 전 무조건적으로 탐욕 정책을 취한다면, 충분한 경험을 하지 못한 채 올바르지 못한 방향으로 빠져 최적의 Q값으로 수렴하지 못할 가능성이 있다. 따라서 agent가 올바른 방향으로 갈 수 있도록, 초기 단계에서 충분한 탐험(exploration)을 할 수 있는 기회를 마련하고자 했고, 이러한 아이디어를 토대로 탄생된 기법이 e-greedy 정책이다. e만큼의 확률로는 탐욕적이지 않은 random한 행동을 선택하게끔함으로써 탐험을 할 수 있도록 유도하고, 1-e만큼의 확률로는 탐욕적인 행동을 하게끔 하는 것이다.

 

이와 같이 SARSA는 Generalized Policy Iteration에서의 정책 평가과정을 e-greedy 기법과 큐함수를 활용한 시간차 예측 알고리즘이라고 할 수 있다. 

 

---

4. Q-learning

 

앞서 언급한 SARSA는 On-Policy 알고리즘의 일종이다. On-Policy 알고리즘이란 현재의 정책을 토대로 행동함으로써 수집된 데이터를 정책의 업데이트에 활용하는 방식으로, 자신이 행동하는대로 학습하는 알고리즘이라고 할 수 있다. 이러한 On-Policy 알고리즘의 경우, 계산속도가 빠르다는 장점이 존재하지만, agent가 충분한 탐험의 과정없이 잘못된 방향으로 학습을 했을 때, 계속 안 좋은 상태에서 벗어나지 못하는 단점이 존재한다.

 

이러한 단점을 보완하는 방법으로 Off-Policy 알고리즘이 있다. Off-Policy 알고리즘은 행동의 기준이 되는 정책과 학습의 기준이 되는 정책을 분리하여 사용하는 방식이다. 이 두 정책을 구분하기 위해, 행동의 기준이 되는 정책을 behavior policy, 학습의 기준이 되는 정책을 target policy라고도 한다. 이 알고리즘은 정책의 업데이트에 있어 agent로 부터 최신으로 수집된 데이터가 아니더라도 사용할 수 있다는 것으며, 이는 곧 데이터 효율성이 크다고 할 수 있다. 

 

SARSA에서는 현재 상태 S에서 e-greedy 정책에 따라 행동 a를 선택하고, 보상 r과 다음 상태 값 s'를 얻는다. 이후에 s'에서 e-greedy 정책에 의거해 다음에 취할 행동 값인 a'를 얻는다. 반면, 큐러닝에서는 다음 상태 S'를 알게 된다면, 또 다시 e-greedy 정책을 바탕으로 행동하는 것이 아니라 해당 상태에서 가장 큰 큐함수를 현재 큐함수의 업데이트에 사용한다. 따라서 현재 상태의 큐함수를 업데이트하기 위해 필요한 샘플은 <s, a, r, s'>이다. 

 

 

결과적으로 위의 식과 같이, 목표로 하는 target Q값과 예측치 간의 차이인 error를 최소화하는 방향으로 Q값을 반복하여 업데이트 한다.